Tail call optimization in Elixir

Lately I've been trying to review some Software Engineering concepts that are widely talked about on a day to day basis, that I may have learned about at university, but that I ended up forgetting.

One of those concepts is Tail Call Optimization. In short, Tail Call Optimization allows you to reduce the number of stack frames your program needs to maintain, in the call stack, for a recursive function by making the recursive call the last call of the function, thus transforming it into a tail recursive function.

A simple recursive function

I'm going to use a very simple example to demonstrate how this type of optimization can be achieved. In this example I'm going to use the factorial function since we can easily write it in a recursive fashion:

defmodule Factorial do
  def compute(0), do: 1
  def compute(number), do: number * compute(number - 1)
end

As one can see, the above fuction (Factorial.compute/1) is recursive, one can see the call to compute(number - 1), however the last function call is actually the multiplication (thanks herulume).

Since this is a recursive function, whenever we call it with a value greater than 0 the system that's running it will have to keep multiple function call stacks.

Let's illustrate what happens when we call Factorial.compute(5) in order to better understand what I mean:

Factorial.compute(5)
= 5 * Factorial.compute(4)
= 5 * (4 * Factorial.compute(3))
= 5 * (4 * (3 * Factorial.compute(2)))
= 5 * (4 * (3 * (2 * Factorial.compute(1))))
= 5 * (4 * (3 * (2 * (1 * Factorial.compute(0)))))
= 5 * (4 * (3 * (2 * (1 * 1))))
= 5 * (4 * (3 * (2 * 1)))
= 5 * (4 * (3 * 2))
= 5 * (4 * 6)
= 5 * 24
= 120

With the illustration above we can attest that the call to Factorial.compute(5) only finishes after all recursive calls are finished, meaning that state for the multiple function calls needs to be maintained and that there's multiple function calls waiting for the result of others in order to finish.

An optimized version

With the function presented above we can now start using Tail Call Optimization to reduce the number of stack frames that need to be kept for this factorial function.

The trick here is simple, for each function, instead of "joining" its work with the result of the recursive call, it will do its part of the work and pass it as an intermediate result to the recursive function call. This way there's no need to maintain the stack frame for the function after the intermediate result is calculated and the recursive call is done, thus the memory space can be collected.

Here's how the tail optimized version of the function looks like:

defmodule Factorial do
  def compute(number, accumulator \\ 1)
  def compute(0, accumulator), do: accumulator
  def compute(number, accumulator), do: compute(number - 1, number * accumulator)
end

Notice how number * compute(number - 1) was changed to compute(number - 1, number * accumulator). The number value is now multiplied with the accumulator and then passed into the recursive call and the function can now be considered a tail recursive function since the last call of the function is the recursive call itself.

Let's do the same exercise we did with the non optimized version above and let's illustrate, once again, what calling Factorial.compute(5) would look like with this version:

Factorial.compute(5)
= Factorial.compute(5, 1)
= Factorial.compute(4, 5)
= Factorial.compute(3, 20)
= Factorial.compute(2, 60)
= Factorial.compute(1, 120)
= Factorial.compute(0, 120)
= 120

It might be a personal opinion, but I do think that it's way easier to reason about this version than the one we explored before.

Measuring performance

At the beggining of this blog post I've explained that this kind of optimization reduces the number of stack frames the applications needs to maintain. This should also mean that the memory footprint of the application is, then, reduced as a direct result of this optimization.

To test this assumption I've decided to put both versions head to head and check two metrics:

• Execution Time
• Memory Usage

In order to measure execution time I simply used the following Elixir function (taken from stackoverflow) which returns the duration of the provided anonymous function call in seconds .

defmodule Benchmark do
  def measure(function) do
    function
    |> :timer.tc
    |> elem(0)
    |> Kernel./(1_000_000)
  end
end

For the memory usage values I took a screenshot of the memory usage reported by Erlang's observer, which you can enable by running :observer.start() on an IEx shell, this should give us a rough idea if memory consumption grows or declines.

Finally, in order to test the calls I ran each one 5 times in a row, back to back, using the following code:

0..4 |> Enum.map(fn _index -> Benchmark.measure(fn -> Factorial.compute(100_000) end) end)

I used the average execution time of these function calls so as to avoid any deviations that might be cause by caching (which didn't happen, but better safe than sorry) and what not.

Results

Now it's time for the results!

In regards to execution time, as expected, both versions reported similar results, with the following times being gathered on an average of 5 runs:

• Non-Optimized Version - 5.244692 seconds
• Optimized Version - 5.172864 seconds

As for the memory load, that's where we actually see the difference of the optimized version!

The image below shows the 5 calls to both the non-optimized (red) and the optimized (blue) version. One can see the spiky pattern of the non-optimized version, meaning that memory was being used by the multiple function calls and then released when the result of the successive recursive calls was achieved, while for the optimized version the memory usage seems to not even grow at all!

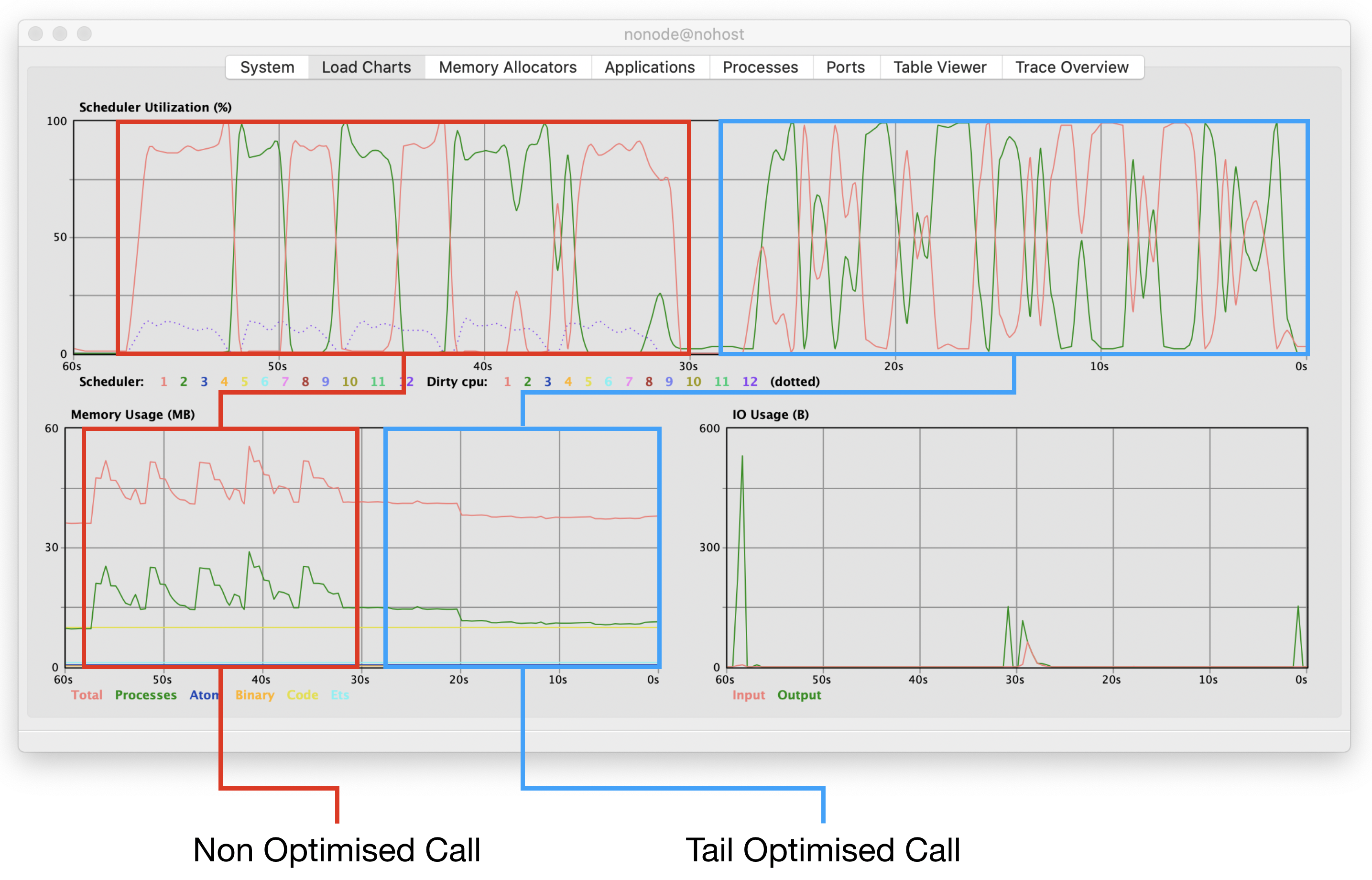
I'd say these are great results!

Conclusion

It's fun to review these type of concepts and try to apply them in a more pratical scenario in order to fully understand how they work and what are its impacts.

As for Tail Call Optimization I'd say it might be a nice, easy and simple way to reduce memory usage in recursive functions, given that you're able to transform them into tail recursive functions, something that might be a very common occurrence in Elixir. I say it might, because converting a body recursive function into a tail recursive function is not always the correct choice, plase read The Seven Myths of Erlang Performance and Fred Hebert's Erlang's Tail Recursion is Not a Silver Bullet to better understand why.

I'm planning on releasing more of these blog posts where I dive into some software development concept and try to explain it using Elixir so stick around and don't forget to keep checking this blog from time to time.

Lastly, thank you, the reader, for taking the time to read this post. If you got any feedback at all I'd encourage you to express it by following one of the links below!

---

• Reddit Discussion
• Hackernews Discussion